Elliptic Curve Cryptography (ECC)

Table of Contents

• Elliptic Curve
• Elliptic Curve over Real Numbers
  • Point Addition
  • Point Multiplication
• Elliptic Curve over Finite Field
  • Point Arithmetic over Finite Field
  • Cyclic Group
• Elliptic Curve in Cryptography
  • Elliptic-Curve Diffie–Hellman (ECDH)

Elliptic Curve

Elliptic curves have the general form:

$$y^2=a{x}^3+b{x}^2+cx+d$$

Weierstrass Form: $y^2=x^3+ax+b$

Montgomery Form: $b{y}^2=x^3+a{x}^2+x$

Twisted Edwards Form: $a{x}^2+y^2=1+d{x}^2{y}^2$

All three forms are equivalent, as there exists bijective mapping of any curves between any two forms.

For any point in the general form $(x,y)$, $y^2=a{x}^3+b{x}^2+cx+d=a(x-r)(x^2+s_1+s_2)$ for some constants $r,s_1,s_2$.

Elliptic Curve over Real Numbers

Denote the curve as $E$.

For some constants $a,b\in \mathbb{R}$, such that $\Delta =4a^3+27b^2\ne 0$, the set of points on the curve is: $$E(\mathbb{R}):=\{(x,y):x,y\in \mathbb{R},y^2=x^3+ax+b\}\cup \{\mathcal{O}\}$$ , where $\mathcal{O}$ is the identity (the point at infinity).

Point Addition

The sum of points $P(x_1,y_1)$ and $Q(x_2,y_2)$ for elliptic curves is $-R=(x_3,y_3)$, where $-R$ is the reflection over the x-axis of $R$, and $R$ is the intersection point of line $\overline{PQ}$ with the curve. If such point does not exists, then the sum $-R=\mathcal{O}$ would be the infinity point.

This operation is commutative, which means that the group $(E(\mathbb{R}),+)$ is an Abelian Group, with the identity being $\mathcal{O}$.

Example with the curve $y^2=x^3+1$, $(1,\sqrt{2})+(-1,0)=(0.5,-\sqrt{1.125})$:

Algebraic Expression of Point Addition

Case $P=\mathcal{O}\vee Q=\mathcal{O}$

There exists only one intersection between the tangent line at $P=Q$ and the curve; hence,

$P=\mathcal{O}⟹-R=Q$, and

$Q=\mathcal{O}⟹-R=P$.

Case $P\ne Q$

$-R=({\lambda }^2-x_1-x_2,-{\lambda }^3+(x_1+x_2)\lambda -c)$, where $\lambda =\frac{y_2-y_1}{x_2-x_1},c=\frac{y_1{x}_2-y_2{x}_1}{x_2-x_1}$.

Case $P=Q\wedge y\ne 0$

$R$ would be the second intersection point of, the tangent line of the curve at $P$. For curve in Weierstrass form, the formula is given as:

$-R=({\lambda }^2-x_1-x_2,-{\lambda }^3+(x_1+x_2)\lambda -c)$, where $\lambda =\frac{3x^2+a}{2y},c=\frac{-x^3+ax+2b}{2y}$.

Case $P=Q\wedge y=0$

$-R=\mathcal{O}$, because there exists only one intersection between the tangent line at $P=Q$ and the curve.

Point Multiplication

Point multiplication is defined to be repeated point addition. Given a point $P$ and an integer $n$, $nP:={\sum }_{i=1}^{n}P$. This could be done efficiently with the double-and-add method.

However, similar to the index, there is no more efficient method of finding $n$ given $P$ and $nP$ in comparison with repeatedly subtracting $P$ from $nP$.

Elliptic Curve over Finite Field

For some prime $p\in \mathbb{Z}$ and some constants $a,b\in {\mathbb{Z}}_p$, such that $4a^3+27b^2\not\equiv 0(\mathrm{mod}p)$, the set of points on the curve is: $$E({\mathbb{Z}}_p):=\{(x,y):x,y\in {\mathbb{Z}}_p,y^2\equiv x^3+ax+b(\mathrm{mod}p)\}\cup \{\mathcal{O}\}$$ , where $\mathcal{O}$ is the identity (the point at infinity).

Point Arithmetic over Finite Field

Point addition over the finite field is similar to point addition over infinite field, with the exception that all operations are done under modulo $p$, and division becomes multiplication with the modular inverse (always exists since the modulo is a prime).

Point multiplication over the finite field is repeated addition, and also can be computed efficiently with the double-and-add method.

Cyclic Group

To generate a cyclic group from $E({\mathbb{Z}}_p)$, choose any point $g\in E({\mathbb{Z}}_p)$, and construct $⟨g⟩$. This cyclic group of order $n$ would be a subgroup of $E({\mathbb{Z}}_p)$. The order of $⟨g⟩$ depends on the choice of $g$, and it must be a divisor of $E({\mathbb{Z}}_p)$ by Lagrange's Theorem.

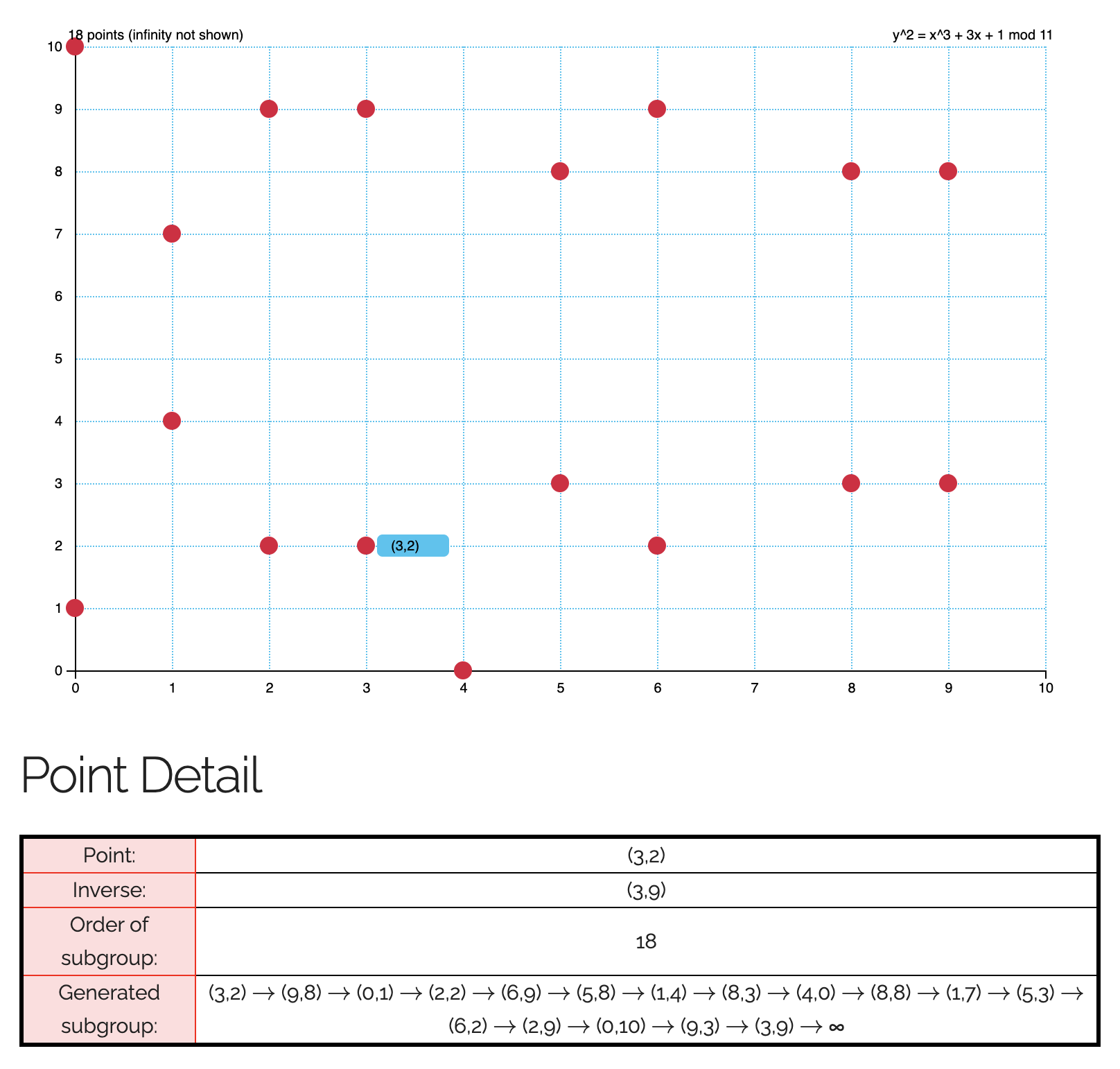(An example of a cyclic group formed)

Elliptic Curve in Cryptography

ECC is based on elliptic curve over the prime finite field.

Elliptic-Curve Diffie–Hellman (ECDH)